Strikeout rate predictions by IP buckets (visuals)

I retrained my SO9 prediction model after scaling pitcher season weights in reverse proportion to the SO9 variance implied by IP. See the previous post for an explanation of how I did this.

The model did not change much. That is good. After many iterations of training, my model has stabilized. It is now consistently splitting the pitcher seasons into three similar sized buckets. But more on that in the next post. For now, I quickly want to explain the graph above.

----

After breaking down my 5,017 pitcher seasons into 5 buckets by IP, I graph the scatter plot for actual vs predicted IP in the 5 series. Also, I graph the trend lines for each data subset.

The graph is a bit messy, but one thing is clear about the five distributions:

• The series for [+∞, 116], [116, 65] and [65, 39] IP have similar distributions
  
• The series for [14, 0] IP shows that my model has very little ability to predict SO9 rates for that series
• The [39, 14] IP series is somewhere in the middle, but closer to the first three series. So I can predict these strikeout rates somewhat well, but still much worse than those with 39+ IP.

This observation reflects the variance estimates from the previous post. Again, my new model has almost exactly the same weights as before. However since the pitcher seasons in the [14, 0] IP range have between 10 and 100 less training weight than the 200 IP pitcher seasons, the new model claims a higher correlation with the data set. I think this makes some sense.

Before I scaled pitcher seasons by inverse SO9 variance estimates, the correlation between my model and the data would swing between 0.6 and 0.4, depending on how much of the lower-IP pitcher seasons data I included. Now, the correlation stays a little below 0.6 (0.5467 in the latest model), regardless of how much of the lower-confidence data I include.

Over the several models that I trained, my ability to predict SO9 for higher-IP pitcher seasons has remained the same. However, models that are trained on 40IP cutoffs, 20IP cutoffs, etc, do very poorly in predicting IP for the pitchers with very low IP.

Therefore now, I can train on all the data, predict SO9 as well as I can for pitcher seasons of all IP, and yet not have the noisy low-confidence data make my correlations look artificially bad. So I'm happy. Now I can move on to something more interesting, like looking at the model that I'm producing more closely.

-----

While you're looking at the graph, there is one more observation worth noting:

• Even for high-confidence (high IP) data, my model consistently fails to predict high-strikeout seasons.

First of all, is this really the case? Let's zoom in to the graph for all high strikeout pitcher seasons. To avoid low-confidence points, I only plot the three series for pitcher seasons with at least 39 IP. Also to get some context and to avoid multiple-endpoint statistical traps, I plot the top 1/3 (by strikeout rates) of all those pitcher seasons. The cutoff ends up at 7.42 SO9:

As the trend lines show, my model does indeed tend to under-predict high strikeout pitcher seasons. My under-predictions increase steadily as actual SO9 increases. I especially under-predict the really high SO9 seasons.

The SO9 >= 10.0 seasons represent 19.3% of the seasons show above (which in turn represent the top 1/3 of all pitcher seasons with significant IP). So the high-strikeout pitcher seasons form a small (1/15) but significant part of my data set. If strikeout rates fluctuated wildly from season to season for individual pitchers, then this would make sense. However, intuitively we know that this is probably not the case. Pitchers like Eric Gagne, Brad Lidge, and others (see previous posts for a complete list of high-strikeout pitcher seasons) show that the ability to record exceptionally high strikeout rates is a repeatable skill.

Figuring out why I fail to predict these high-strikeout seasons is beyond the scope of this post. However I suggest some ideas why this could be the case:

1. Exceptionally high strikeout totals can not be predicted only from pitch data.
2. Relationships between pitch data and strikeout rate are not linear, therefore my piecewise-linear solutions are bound to under-estimate outputs for high-end inputs.
3. The algorithm I use to generate my models performs a smoothing operation in the data. Perhaps I am losing something valuable because of the smoothing of what look like outliers.

All three explanations make sense to me. However two of them are pretty easy to look into.

----

I retrained my model with smoothing turned off. No difference. I trained a model that only looks at fastball velocity and pitcher handedness. Again, turning off smoothing made no difference. So scratch explanation #3.

Reason #2 was a bit harder to evaluated.

First of all, I need to re-iterate that the average fastball speed (FB_fg_vel as I referenced it in early posts) is the single most predictive feature that I have. There is a 0.22 correlation between observed strikeout rate (actual SO9) and fastball speed. If I train a piecewise linear model with this single feature, I can get a correlation of 0.48. So actually, my model for predicting strikeout rate from pitch data is mostly a model for predicting strikeout rate from fastball speed.

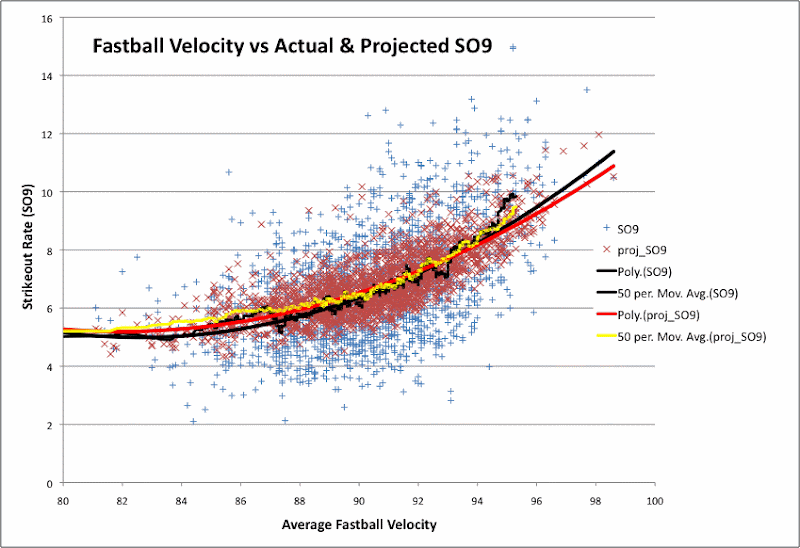
Below, I show the relationship between fastball speed and observed strikeout rates. Also I plot my predicted strikeout rates. To make the graph less cluttered, I only plotted data from pitcher seasons with 65+ IP.

Along with the scatter plot for real and predicted strikeout rate, I also included:

• a trend line for the data, fit to a quadratic function
• a 50-point moving average of the strikeout rate (ranked by fastball speed)

Again, you can see that my predictions are much lower than actual strikeout rates for pretty much all the high-strikeout pitcher seasons. There are quite a few blue points in the top right section of the graph (>92 mph, >10 SO9) that the red points don't reach at all.

However, the trend line for my predictions and the trend line for the actual values do not differ by much, even at the high end of the fastball scale. At most, my quadratic of best fit is 0.5 SO9 below the quadratic for the actual values. The 50-point average seems to jump up for the actual values somewhere around 95 mph. But the jump isn't big enough to be sure if it's significant.

This all leads me back to reason #1. I do not have the features in my model, in order to predict really high strikeout rates. Also, I'm pretty sure I won't get there by looking at the average fastball speed on a different scale. The answer could be hidden in something I already have (but I don't present properly to the model), like the speed differential between a pitcher's fastball and change-up. Or it could be something that I haven't imported yet.

As always, the more I think I learn about baseball, the more questions I seem to raise to myself. But that is the nature of the beast.